Naked Subset

This is where two squares in the same block, row or column contain the same two possibilities. This also works where three squares contain no more than three possibilities or where four squares contain no more than four possibilities. Consider the following block:

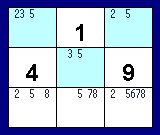
The highlighted squares contain as possibilities (2, 3, 5) (2, 5) and (3, 5). We can deduce that these three squares must contain a 2, 3 and 5 (although we don't know which square contains which number). Therefore we can eliminate these numbers as possibilities from the other squares in this same block (i.e. the 2 and 5 from the bottom left-hand square, the 5 from the bottom middle square and the 2 and 5 from the bottom right-hand square). Doing this leaves a naked single of 8 in the bottom left-hand square, which means this square must contain a 8.

<< Prev

Strategies

Next >>